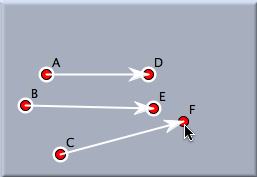
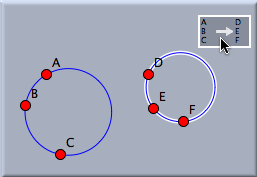
Moebius TransformationMöbius TransformationMathematically, perhaps the most interesting transformation available in Cinderella is the Möbius transformation. This is a transformation with the property that circles and lines are again mapped to circles and lines. Any rotation, translation, or similarity can be considered a special case of a Möbius transformation, whereas neither an affine transformation nor a projective transformation is a Möbius transformation. A Möbius transformation is defined by three preimage/image pairs of points. Defining a Möbius transformation in Cinderella is analogous to the creation of a similarity, though with six required points instead of four. The following two pictures demonstrate how a circle is mapped under a Möbius transformation. Since the Möbius transformation in the picture maps A → D, B → E, C → F, a circle through A, B, C is mapped to a circle through D, E, F.
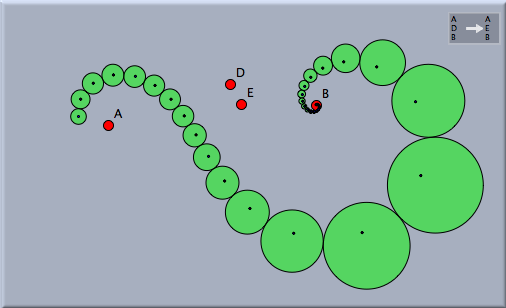
If one iterates a Möbius transformation, the sequence of mapped pictures forms a mathematically and aesthetically very interesting pattern that can be considered a generalization of a logarithmic spiral. The following picture shows the image of an iterated Möbius transformation applied to a single circle and its center.
A Möbius transformation usually has two distinct fixed points. In the above drawing these fixed points have been constructed explicitly by making sure that the transformation maps A to itself and B to itself.
Contributors to this page: Kortenkamp
,
Richter
,
Kohler
and
Kramer
. The content on this page is licensed under the terms of the License. |
Login |